Kosinusna teorema

Kosinusna teorema je formula koja se koristi za rešavanje trougla u trigonometriji u ravni:

$c^2=a^2+b^2-2ab\cos C,$

gde je C ugao nasuprot stranice c, tj. ugao između stranica a i b trougla.

U sfernoj trigonometriji to je formula za rešavanje sfernog trougla:

$\cos c=\cos a\cos b+\sin a\sin b\cos C,\cos C=-\cos A\cos B+\sin A\sin B\cos c,$

gde je a strana nasuprot ugla A, strana b je nasuprot ugla B, a strana c je nasuprot ugla C.

Trigonometrija u ravni

Kosinusna teorema ima istu analitičku formu nezavisno od toga da li je dati trougao oštrougli (sl.1) ili tupougli (sl.2). Međutim, obično se posebno dokazuje svaki od ta dva slučaja, kao što je urađeno u dokazu koji sledi.

Sl.1. Oštrougli trougao

Kosinusna teorema

U svakom trouglu je $a^2=b^2+c^2-2bc\cos \alpha ,$ gde je nasuprot stranice a ugao α.

Dokaz

Na slici desno (sl.1) dat je oštrougli trougao ABC sa visinom CD. Iz pravouglih trouglova BCD i ACD prema Pitagorinoj teoremi je $a^2=h^2+(c-p{)}^2,h^2=b^2-p^2,$ a otuda zamenom dobijamo prvo $a^2=b^2+(c^2-2pc+p^2)-p^2,$ a onda $a^2=b^2+c^2-2pc.$ Iz pravouglog trougla ACD dobijamo $p=b\cos \alpha ,$ i zamenom u prethodnu jednakost $a^2=b^2+c^2-2bc\cos \alpha ,$ što je i trebalo dokazati.

Sl.2. Tupougli trougao

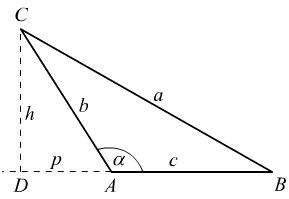
Dalje, na slici (2) levo, dat je tupougli trougao ABC, sa uglom α u temenu A, većim od pravog ugla (90°). Visina CD = h pada na produžetak stranice AB u tačku D tako da je D-A-B, te je spoljašnji ugao CAD = 180°-α. U trouglu CAD je

DA = $p=b\cos (180^o-\alpha )=-b\cos \alpha .$

Sa druge strane, trouglovi BCD i ACD su pravougli i, prema Pitagorinoj teoremi imamo $a^2=h^2+(c+p{)}^2,h^2=b^2-p^2,$ pa zamenom dobijamo

$a^2=b^2-p^2+(c^2+2pc+p^2)=b^2+c^2+2pc,$ tj.

$a^2=b^2+c^2-2bc\cos \alpha ,$ kao što je i trebalo dokazati. Kraj dokaza.

Kosinusna teorema se može dokazati jednostavno i bez razmatranja različitih rasporeda koristeći vektorski račun. U gornjim oznakama,

$a^2=\stackrel{2}{\overrightarrow{BC}}=(\overrightarrow{AC}-\overrightarrow{AB}{)}^2=\stackrel{2}{\overrightarrow{AC}}-2\overrightarrow{AB}\cdot \overrightarrow{AC}+\stackrel{2}{\overrightarrow{AB}}=b^2-2bc\cos \alpha +c^2.$

($\cdot$ označava skalarni proizvod.)

Drugačijim označavanjem trougla, dobićemo i ostale dve formule, koje se zajedno sa navedenom nazivaju kosinusna teorema: $b^2=c^2+a^2-2ca\cos \beta ,c^2=a^2+b^2-2ab\cos \gamma .$ Kada je, na primer ugao u temenu C = γ=90°, zbog cos(90°)=0, poslednja formula postaje $c^2=a^2+b^2,$ tj. Pitagorina teorema je poseban slučaj kosinusne teoreme. Pored toga, kosinusna teorema ima još nekih važnih posledica.

Teorema 2

Kvadrat bilo koje stranice trougla je manji, jednak, ili veći od zbira kvadrata ostale dve stranice, zavisno od toga da li je suprotni ugao oštar, prav, ili tup.

Dokaz

Ako je $\alpha <90^o,$ tada je $\cos \alpha >0$ i $a^2=a^2+b^2-2ab\cos \alpha <b^2+c^2.$

Ako je $\alpha =90^o,$ tada je $\cos \alpha =0$ i $c^2=a^2+b^2.$

Ako je $\alpha >90^o,$ tada je $\cos \alpha <0$ i $a^2=a^2+b^2-2ab\cos \alpha >b^2+c^2.$ Kraj dokaza.

Važi i suprotna teorema.

Teorema 3

Ugao trougla je oštar, prav, ili tup zavisno od toga da li je kvadrat suprotne stranice trougla redom manji, jednak, ili veći od zbira kvadrata ostale dve strane.

Dokaz

Sledi iz kosinusne teoreme $\cos \alpha =\frac{b^2+c^2-a^2}{2bc}.$

Ako je $a^2<b^2+c^2,$ tada je $\cos \alpha >0,$ i prema tome $\alpha <90^o.$

Ako je $a^2=b^2+c^2,$ tada $\cos \alpha =0,$ tj. $\alpha =90^o.$

Ako je $a^2>b^2+c^2,$ tada je $\cos \alpha <0,$ tj. $\alpha >90^o.$ Kraj dokaza.

Teorema 4

U bilo kojem paralelogramu zbir kvadrata dijagonala jednak je zbiru kvadrata sve četiri njegove strane.

Sl.3. Paralelogram

Dokaz

Na slici (3) desno, dat je paralelogram ABCD sa dijagonalama AC i BD i uglom BAD = α.

Tada je $\stackrel{2}{\stackrel{‾}{AC}}+\stackrel{2}{\stackrel{‾}{BD}}=2\stackrel{2}{\stackrel{‾}{AB}}+2\stackrel{2}{\stackrel{‾}{BC}}.$ Naime, kako je ugao CBA = 180°-α, prema kosinusnoj teoremi iz trouglova ADB, ABC dobijamo $\stackrel{2}{\stackrel{‾}{BD}}=\stackrel{2}{\stackrel{‾}{AD}}+\stackrel{2}{\stackrel{‾}{AB}}-2\overline{AB}\cdot \overline{AD}\cdot \cos \alpha ,$

$\stackrel{2}{\stackrel{‾}{AC}}=\stackrel{2}{\stackrel{‾}{AB}}+\stackrel{2}{\stackrel{‾}{BC}}-2\overline{AB}\cdot \overline{BC}\cdot \cos (180^o-\alpha )$

$=\stackrel{2}{\stackrel{‾}{AB}}+\stackrel{2}{\stackrel{‾}{BC}}+2\overline{AB}\cdot \overline{AD}\cos \alpha ,$ jer je $\overline{BC}=\overline{AD}.$ Sabiranjem ovih jednačina, dobijamo

$\stackrel{2}{\stackrel{‾}{AC}}+\stackrel{2}{\stackrel{‾}{BD}}=2\stackrel{2}{\stackrel{‾}{AB}}+2\stackrel{2}{\stackrel{‾}{BC}},$ što je i trebalo dokazati. Kraj dokaza.

Povezano

• Matematika
• Geometrija
• Planimetrija
• Trigonometrija
• Trougao
• Sinusna teorema
• Tangensna teorema
• Rešavanje trougla

Vanjske veze

• Kosinusna teorema na -{mathworld.wolfram.com}- Šablon:En
• Kosinusna teorema na -{www.cut-the-knot.org}- Šablon:En