Hiperbola

Za stilsku figuru, pogledajte Hiperbola (književnost)

Hiperbole x²-y²=1 i y²-x²=1

Hiperbola i njena 2 fokusa

Vrste konusnih presjeka (kružnica, elipsa, parabola i hiperbola)

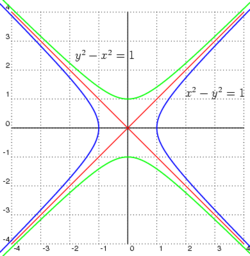
Hiperbola (starogrč. ύπερβολή, preterivanje) u matematici je algebarska kriva drugog reda u ravni, data sledećom jednačinom: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$. Sastoji se iz dva simetrična dela, ima dva fokusa i dve asimptote date jednačinom $ay\pm bx=0$. Tačka preseka asimptota predstavlja centar simetrije hiperbole.

Hiperbola, zajedno sa parabolom i elipsom, predstavlja tri tipa konusnih preseka. Konusni preseci se dobijaju u preseku ravni sa konusnom površinom (konusna površina se proteže u oba pravca).

Jednačine hiperbole

Parametarska jednačine hiperbole je: $\{\begin{array}{c}x=a\sec \alpha \\ y=b\tan \alpha \end{array}$

U Dekartovom koordinatnom sistemu, hiperbola se opisuje jednačinom:

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$

Osobine

Postoje dve važne osobine fokusa hiperbole $F_1,F_2$:

1. Za svaku tačku hiperbole R, važi (d je rastojanje): $\mid d(P,F_1)-d(P,F_2)\mid =2aa\in ℝ$
   Ovo svojstvo omogućava i sledeću definiciju hiperbole: Geometrijsko mesto tačaka u ravni, za koje je apsolutna vrednost razlike rastojanja od bilo koje tačke do dve fiksne tačke u istoj ravni (dva fokusa), konstantna.
2. Tangenta na svaku tačku hiperbole R predstavlja bisektrisu $\mathrm{\angle }{F}_{1}P{F}_2$.

Vanjske veze

• Informacije o hiperboli